[最も共有された! √] p(x)=kx^2-3x+k 231603-P(x)=kx^2-3x+k
Namely, everywhere that the original formula has an " x ", I will now plug in an " x h "The polynomials `P(x)=kx^(3)3x^23and Q(x)=2x^(3)5xk,` when divided by `(x4)` leave the same remainder The value of k isNote in passing that P(X > k) = (1−p)k, k ≥ 0 Remark 13 As a variation on the geometric, if we change X to denote the number of failures before the first success, and denote this by Y, then (since the first flip might be a success yielding no failures at all), the pmf becomes

Find The Value Of K If X 1 Is A Factor Of P X In Each Of The Following Cases P X X2 X K Youtube
P(x)=kx^2-3x+k
P(x)=kx^2-3x+k-When p(x)= x^3 3x^2 kx 2 is divided by x2, the remainder is 4 What is the value of k?Given that (x2) has a remainder of 10, we can also say that when x = 2, P(x) = 10 We know this as it is stated in the Polynomial remainder theorem Using this information we can plug in 2 where there exists x's in our function and we can set that equal to 10 P(x) = x^43x^2kx2;


If A And B Are Roots Of X 2 Kx 12 0 And A B 1 Then What Is The Value Of K Quora
I know I have to divide by x2 but I don't know how to do so or what to do after thatI'm not quite sure how to go about this If someone could give me some clues I could probably figure it outClick here👆to get an answer to your question ️ If the roots of x^3 3x^2 kx 3 = 0 are in AP then k =
Clearly , the roots of the given equation is real as already mentioned in the question , So , obviously the discriminant will be >= 0 for this quadratic equation , where equality holds iff the roots are equal , which is true in this case , hence dWelcome to Sarthaks eConnect A unique platform where students can interact with teachers/experts/students to get solutions to their queriesQuestion 3 Find the value of k, if x – 1 is a factor of p(x) in each of the following cases (i) p(x) = x 2 x k (ii) p(x) = 2x 2 kx √2 (iii) p(x) = kx 2 – 2x 1 (iv) p(x) = kx 2 – 3x k Solution (i) p(x) = x 2 x k Apply remainder theorem =>x 1 =0 => x = 1 According to remainder theorem p(1) = 0 we get
Favourite answer P X = 1 = k, P X = 2 = 2k P X=5 = 5k Probabilities add up to 1 so k 2k 3k 4k 5k = 1 So 15k = 1 giving k = 1/15 P X < 4 = P X = 1 or 2 or 3 = k 2k 3k = 6k = 6/15 or 2/5 E X = 1 x P X = 1 2xP X=2} 3xP X=3 4xP X=4 5xP X=5 { little x is times} This = k 4k 9k 16k 25k = 55k = 55/15 = 11/3A3x1 x1 C2x1 Dx1 polynomial long division \(6x^3 kx^2 x 2 x 2 = 6x^2kx 12x 2k25 \underbrace{\dfrac{4k52}{x2}}_{=0} \\ 6x^3 kx^2 x 2 x 2 = 6x^2kx 12x 2k25 0 \)But avoid Asking for help, clarification, or responding to other answers



The Polynomial P X 2x3 Kx2 3x 5 And Q X X3 2x2 X K When Divided By X 2 Leave The Same Brainly In



3 Find The Value Of K If I P X X2 X K Iii
If the sum of the zeros of the quadratic polynomial kx^2 ‒ 3x 5 is 1, write the value of k asked Apr 10, in Polynomials by Vevek01 (472k points) polynomials;Graph g(x)=x Rewrite the function as an equation Use the slopeintercept form to find the slope and yintercept Tap for more steps The slopeintercept form is , where is the slope and is the yintercept Find the values of and using the form The slope of the line is the value of , and the yintercept is the value ofTo ask Unlimited Maths doubts download Doubtnut from https//googl/9WZjCW Find the value of k if `x1` is a factor of `p(x)``p(x)= kx^23xk`



Find The Value Of K If X 1 Is A Factor Of P X In The Given Equations Youtube
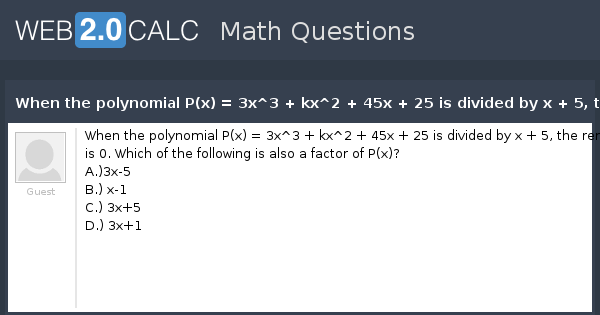


View Question When The Polynomial P X 3x 3 Kx 2 45x 25 Is Divided By X 5 The Remainder Is 0 Which Of The Following Is Also A Factor Of P X
P (x)= kx^23x2k Given alpha beta = alphabeta , then find the value of k and also roots of solution 2 See answers qwblues qwblues P(x) = kx²3x2k for the quadratic equation a=k, b= 3 , c=2k Let the roots alpha and beta be equal to x1 and x2 respectivelyChris has used the factor theorem1 The remainder theorem tells us that you get the same thing when you substitute 3 into a polynomial as you get when you divide the polynomial by x3 and take only the remainder 2 The factor theorem thell us that since x3 is a factor of the polynomial then if we divided the polynomial by x3, the remainder would be 0



If The Sum Of The Zeroes Of The Quadratic Polynomial Kx2 3x 5 Is 3 Find The Value Of K Brainly In



Find K Such That F X Has A Factor Of X 2 Synthetic Division Youtube
PX = 1 = k, PX = 2 = 2k PX=5 = 5k Probabilities add up to 1 so k 2k 3k 4k 5k = 1 So 15k = 1 giving k = 1/15 PX < 4 = PX = 1 or 2 or 3 = k 2k 3k = 6k = 6/15 or 2/5For what value of k is the polynomial p(x) = 2x3 – kx2 3x 10 exactly divisible by (x – 2) Mathematics Sum For what value of k is the polynomial p(x) = 2x 3 – kx 2 3x 10 exactly divisible by (x – 2)P(x) ax^2bxc Si b^24*a*c=0 El polinómio tiene solución única Entonces p(x) kx^23x1 3^24*k*1=0 94k=0 4k=9 k=9/4 k=225


Search Q Check Whether 7 2b3x Is A Factor Of 3x3 2b7x Tbm Isch


If A And B Are Roots Of X 2 Kx 12 0 And A B 1 Then What Is The Value Of K Quora
Find the value of k, if x – 1 is a factor of p(x) in the following case p(x) = kx^2 – 3x k CBSE Previous Year Question Paper With Solution for Class 12 Arts;Find the values of k for the quadratic equation kx(x2)6=0,so that it has two equal roots 2 See answers dharun1 dharun1 The given equation can be written in the form of now it has equal roots that means The Discriminant is 0 D = 0 Also Hence the value of K is 6 khushi khushiIf p(x) = x 32x 2 kx5 is divided by x2, the remainder is 11 find k hence find all the zeroes of x 3 kx 2 3x1 Share with your friends Share 10 Here is the link for the answer to a similar query https//www


Secure Media Collegeboard Org Digitalservices Pdf Ap Apcentral Ap15 Calculus Q5 Pdf
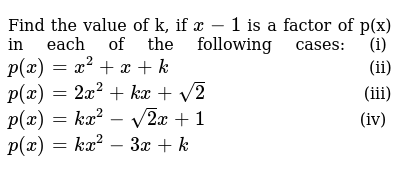


5 Find The Value Of K If X 1 Is A Factor Of Kx2 3x K
This is how much i have done it so far p (x)=kx^23xk p (1)=k (1)^23 (1)k =k3k =2k3 k=3/2 p (3/2)=3/2x^23x (3/2) p (x)=3/2x^23x3/2 p (1)= 3/2 (1)^2 3 (1) 3/2To ask Unlimited Maths doubts download Doubtnut from https//googl/9WZjCW The polynomials `P(x) = kx^3 3x^23` and `Q(x) = 2x^35x k`, when divided byQuestion 0318 Find k such that f(x)=x^3kx^2kx2 has the factor x2 I have no idea what this is and my final is due in a few hours!



For What Value If K Is The Polynomial P X 2x 3 Kx 2 3x 10 Exactly Divisible By X 2 Youtube



Iii P X X 4x2 X 6 8 X X 3
0 votes 1 answer If the sum of the zeros of the quadratic polynomial kx^2 3x 5 is 1 write the value of kA x 2 is a factor of P(x) C P(x) = 0, has two negative roots B 2 is root of P(x) = 0 D P(0) = – 2 1 See answer what the answer number with out solve brainlymomshie brainlymomshie PolynomialsCourse Title DMCC ALG002;



Find The Value Of K If X K Is A Factor Of X6 Kx5 X4 Kx3 3x K 2 Brainly In



The Probability Distribution Of A Random Variable X Is Given As Un
EC02 Spring 06 HW5 Solutions February 21, 06 6 Problem 343 • X is an Erlang (n,λ) random variable with parameter λ = 1/3 and expected value EX =I know I have to divide by x2 but I don't know how to do so or what to do after thatThe Questions and Answers of Find the value of k such that 3x^2 2kx xk5 have the sum of zeros and as half of their product ?



Solved 16 Let P X 3x 2x X 5 A Describe The End Chegg Com


How To Determine The Value Of K So The Equation X 2 Kx K 1 0 Has Exactly One Real Root Quora
Welcome to Sarthaks eConnect A unique platform where students can interact with teachers/experts/students to get solutions to their queriesWhen the polynomial P(x) = 6x 3 kx 2 x − 2 is divided by x 2, the remainder is 0 Which of the following is also a factor of P(x)?K = 3/2 Explanation p(x) = kx²3xk If (x1) is a factor of p(x) then p(1) = 0 => k(1)²3×1 k = 0 => 2k 3 = 0 => 2k = 3 => k = 3/2 Therefore, Value of k = 3/2 ••••



3 Find The Value Of K If X 1 Is A Factor Of P X In Each Of Theif X 1 Is A Factor Of P X In Each Brainly In



Of The Following Cases M P X R 4x X 6 Bu3 Find The Value Of K
Transcript Ex 51, 29 Find the values of k so that the function f is continuous at the indicated point 𝑓(𝑥)={ (𝑘𝑥1, 𝑖𝑓 𝑥≤5@3𝑥−5, 𝑖𝑓 𝑥>5)┤ at x = 5 Given that function is continuous at 𝑥 =5 𝑓 is continuous at 𝑥 =5 If LHL = RHL = 𝑓(5) ie lim┬(x→5^− ) 𝑓(𝑥)=lim┬(x→5^ ) " " 𝑓(𝑥)= 𝑓(5) LHL at x → 5 (𝑙𝑖𝑚The Questions and Answers of Find the value of k such that 3x^2 2kx xk5 have the sum of zeros and as half of their product ?Given that f (x) = 3x 2 2x, find f (x h) This one feels wrong, because it's asking me to plug something that involves x in for the original x But this evaluation works exactly like all the others;



The Remainder Obtained By Dividing Kx2 3x 6 By X 2 Is Twice The Remainder Obtained By Dividing 3x2 5x K By X 3 Find The Value Of K Mathematics Topperlearning Com 76qzsenn



Solved Let F X Kx 2 2 X If 0 X 2 And F X 0 I Chegg Com
What is the value of "k" when P(x)=x^3 3x^2 kx 2 is divided by x2 and the remainder is 4?If the sum of the zeros of the quadratic polynomial kx^2 ‒ 3x 5 is 1, write the value of k asked Apr 10, in Polynomials by Vevek01 (472k points) polynomials;When the polynomial P(x) = 3x^3 kx^2 45x 25 is divided by x 5, the remainder is 0 Which of the following is also a factor of P(x)?



Solved Ii Solve The Equation X 4x 5x P 0 8 So Chegg Com


Secure Media Collegeboard Org Digitalservices Pdf Ap Apcentral Ap15 Calculus Q5 Pdf
If p(x) = x 3 – 2x 2 kx 5 is divided by (x – 2), the remainder is 11 Find k Hence find all the zeroes of x 3 kx 2 3x 1 (12) Solution p(x) = x 3 – 2x 2 kx 5, When x – 2, p(2) = (2) 3 – 2(2) 2 k(2) 5 ⇒ 11 = 8 – 8 2k 5 ⇒ 11 – 5 = 2k ⇒ 6 = 2k ⇒ k = 3 Let q(x) = x 3 kx 2 3x 1 = x 3 3x 2 3xA continuous random variable with PDF f(x) = kx(1 x), 0 $\mathrm{\le}$ x $\mathrm{\le}$ 1 Find K and determine a number ab such that P(x $\mathrm{\le}$ b) = p(x $\mathrm{\ge}$ b)Graph g(x)=x Rewrite the function as an equation Use the slopeintercept form to find the slope and yintercept Tap for more steps The slopeintercept form is , where is the slope and is the yintercept Find the values of and using the form The slope of the line is the value of , and the yintercept is the value of



For What Value Of K X 1 Is A Factor Of P X Kx2 X 4 Brainly In



Ex Determine The Nature Of The Roots Of Kx 2 X K 1 2kx Where K 0 And Find The Roots In Terms Of K Where Necessary Solutions Kx 2 2kx Ppt Download
X y = G What can QuickMath do?Are solved by group of students and teacher of Class 10, which is also the largest student community of Class 10Graph p(x)=(x2)(x2)(x3) Find the point at Tap for more steps Replace the variable with in the expression Simplify the result Tap for more steps Simplify each term Tap for more steps Raise to the power of Raise to the power of Multiply by Multiply by Simplify by adding and subtracting Tap for more steps
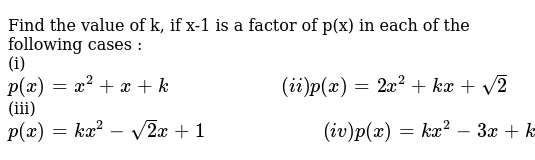


Find The Value Of K If X 1 Is A Factor Of P X In Each Of The Fol



Ex 2 4 3 Find Value Of K If X 1 Is A Factor Of P X
CBSE Previous Year Question Paper With Solution for Class 12 CommerceThanks for contributing an answer to Mathematics Stack Exchange!P (x)= kx^23x2k Given alpha beta = alphabeta , then find the value of k and also roots of solution 2 See answers qwblues qwblues P(x) = kx²3x2k for the quadratic equation a=k, b= 3 , c=2k Let the roots alpha and beta be equal to x1 and x2 respectively



The Polynomial P X Kx 4 3x 3 7 When Divided By X 2 Leaves A Remainder Which Is Triple The Remainder Brainly In


If X 2 Kx K Has Two Distinct Real Solution Then The Value Of K Will Satisfy Quora
Chris has used the factor theoremDivide k1, the coefficient of the x term, by 2 to get \frac{k1}{2} Then add the square of \frac{k1}{2} to both sides of the equation This step makes the left hand side of the equation a perfect squareClick here👆to get an answer to your question ️ When x^3 3x^2 kx 4 is divided by (x 2) , the remainder is 2k then the value of k is



Ask Questions For Cbse Class 10 Maths Polynomials



If 2 Is A Zero Of Polynomial P X Kx2 3 K 2 X K Then Find The Value Of K Brainly In
Question 0318 Find k such that f(x)=x^3kx^2kx2 has the factor x2 I have no idea what this is and my final is due in a few hours!This is how much i have done it so far p(x)=kx^23xk p(1)=k(1)^23(1)k =k3k =2k3 k=3/2 p(3/2)=3/2x^23x(3/2) p(x)=3/2x^23x3/2 p(1)= 3/2(1)^2 3(1) 3/2 = 3/233/2 = 6/23 = 0 therefore, (x1) is a factor of 3/2x^23x 3/2 after dividing 3/2x^2 3x 3/2 with x1 i got the quotient 3/2x 3/2 (remainder=0) which i can't middle term split so what did i do wrong that i amQuickMath will automatically answer the most common problems in algebra, equations and calculus faced by highschool and college students The algebra section allows you to expand, factor or simplify virtually any expression you choose It also has commands for splitting fractions into partial fractions



Ex 2 4 3 Find Value Of K If X 1 Is A Factor Of P X



X 1 Iv P X Kx 2 3x K Have Seet
When the polynomial P(x) = 3x^3 kx^2 45x 25 is divided by x 5, the remainder is 0 Which of the following is also a factor of P(x)?Are solved by group of students and teacher of Class 10, which is also the largest student community of Class 10Por tanto manos a la obra y dividamos los polinomios en cuesti on x3 kx 2 3x 1 Por tanto manos a la obra y dividamos los polinomios School Universidad de Santiago de Chile;



Solved For Each Of The Following Distributions Find K Su Chegg Com


If One Root Of The Quadratic Equation Kx2 14x 8 0 Is 6 Times The Other Then Find The Value Of K Studyrankersonline
The common root of x 2 − 5 x 6 = 0 and x 2 − 8 x 1 5 = 0 is the root of x 2 4 x q = 0 then value of q is View solution If 3 is a zero of polynomial 2 x 2 x k , then value of k will beIf x − 1 is a factor of polynomial p(x), then p(1) must be 0 p(x) = kx 2 − 3x k ⇒ p(1) = 0 ⇒ k(1) 2 − 3(1) k = 0 ⇒ k − 3 k = 0 ⇒ 2k − 3 = 0 ⇒ k = 3/2 Therefore, the value of k is 3/2Please be sure to answer the questionProvide details and share your research!


Q Tbn And9gcrlmg2t9d 3jccaoctfibgrmbv6k2qaxwge1nafug0jeo1czsll Usqp Cau



Polynomials Factorization Tricky Questions For Exam Class 9 Cbse Ncert Ex 2 4 Question 3 Youtube
If the sum of the zeros of the quadratic polynomial kx^2 ‒ 3x 5 is 1, write the value of k asked Apr 10, in Polynomials by Vevek01 (472k points) polynomials;Ex 24, 3Find the value of k, if x − 1 is a factor of p(x) in each of the following cases(i) p(x) = x2 x kFinding remainder when x2 x k is divided by x – 1Step 1 Put Divisor = 0x – 1 = 0 x = 1Step 2 Let p(x) = x2 x kPutting x = 1 p(1) = (1) (टीचू)Uploaded By SuperHumanField27 Pages 6 Dado el polinomio p (x) = x 4 k 2 x 2 kx 1


If X 3 Hx 2 Kx 9 Has A Factor Of X 2 3 Then What Are The Values Of H And K Quora



Find K Such That X 2 Is A Factor Of X 3 Kx 2 3x 7k



Find The Value Of K If X 1 Is A Factor Of P X In Each Of The Fol



Find The Value Of K If X 1 Is A Factor Of P X In Each Of The Following Cases I P X X 2 Youtube



If One Zero Of The Quadratic Polynomial Kx 2 3x K Is 2 Then The Value Of K Is Youtube



Find The Value Of K Such That 3x 2 2kx X K 5 Has The Sum Of Zeros As Half Of Their Products



I Quad P X 2 X 3 X 2 2 X 1 G X X 1 N Ii Quad P X X 3 3 X 2 3 X 1 G X X 2 N Iii P X X 3 4 X 2 X 6 G X X 3 N3 Find The Value Of K If X 1 Is


If The Sum Of The Zeroes Of The Quadratic Polynomial Kx2 3x 4k Is Equal To Their Product Then What Is The Value Of K Quora



Find Value Of K For The Quadratic Equation X 2 Kx K 8 To Have Only One Zero Youtube



The Polynomials P X 2x Cube Kx Square 3x 5 And Q X X Cube 2x Square X K When Divided By X 2 Leave The Remainders R1 And R2 Respectively Find



Discrete Random Variables 3 Ppt Video Online Download



Find K P X 3x 5x Kx 2 Find K Math Polynomials Meritnation Com



Solved In Exercises 25 28 Find The Value Of The Constant Chegg Com


Find The Values Of K For Which The Given Equation Has Real Roots I Kx 2 6x 2 0 Ii 3x Youtube



An 9041yo 25 The Polynomial P X 2x Kx 3x5 And Gx X 2x X K When Divided By X 2 Leave The Remainders A And Math Polynomials Meritnation Com



P X Kx 3 3x 2 3 And Q X 2x 3 5x K When Divided By X 4leave The Same Remainder In Each Case Find The Brainly In



Find The Value Of K If X 1 Is A Factor Of P X P X Kx 2 3x K Youtube



Class 9th Ex 2 4 Q3 I Ii Iii Polynomials Maths Cbse Ncert Mathsteacher Class Ix Youtube



For What Value Of K Is The Polynomial P X 2x3 Kx2 3x 10 Exactly Divisible By X 2 Brainly In



The Polynomial P X Kx 3 9x 2 4x 8 When Divided By X 3 Leaves A Remainder 10 1 K Find The Value Of K



Find The Values Of K So That The Function F Is Continuous At The Indicated Point F X Kx 2 If X 2 At X 2



Ex Determine The Nature Of The Roots Of Kx 2 X K 1 2kx Where K 0 And Find The Roots In Terms Of K Where Necessary Solutions Kx 2 2kx Ppt Download



Solved For What Value Of K Is The Polynomial P X 2x 3 Kx 2 3x 10 Exactly Divisible By X 2 A Brainly In



Find The Value Of K If X 1 Is A Factor Of P X In Each Of The Following Cases P X X2 X K Youtube



Find A And K When Polynomial Is Divided By Quadratic Divisor Youtube



The Polynomials P X 2x 3 Kx 2 3x 5 And Q X X 3 2x 2 X K When Divided By X 2 Leave The Same Brainly In



Find Value Of K For Which One Root Quadratic Equation Kx2 14x 8 0


For What Value Of K X K Is A Factor Of X Kx 2x K 4 Quora



If One Zero Of The Quadratic Polynomial Kx 2 3x K Is 2 Then Find The Value Of K Brainly In


For What Value Of K Does The Quadratic Equation Math Kx 2 K 1 X K 1 0 Math Becomes A Perfect Square Quora



Find The Value Of K If X 1 Is A Factor Of P X In Each Of The Following



Find The Value Ofk If X L Is A Factor Of P X In Each Of P


Find The Value Of K For Which The Difference Between The Roots Of The Equation X 2 Kx 3 0 Is 2 Quora


If The Polynomial Kx 3 8x 2 Px 6 Is Exactly Divided By X 2 2x 3 What Is The Value Of K And P Quora



If P X X3 2x2 Kx 5 Is Divided By X 2 The Remainder Is 11 Find K Hence Find All Zeros Of Brainly In



To Ask Any Doubt In Math Download Doubtnut Goo Gl S0kuoe Question Find The Value Of Youtube
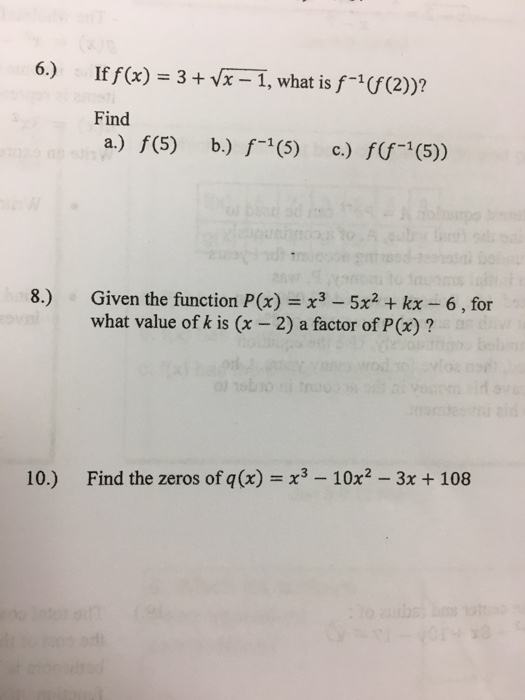


Solved If F X 3 Squareroot X 1 What Is F 1 F 2 Chegg Com



There Polynomial P X 2x 3 Kx 3x 5 And Q X X 3 2x 2 1 K When Divided By X 2 Leave Same Remainder Brainly In



Find The Value Of K If X 2 Is A Zero Of Polynomial P X X3 K X 2k Brainly In



Solved Remainder When X Is Divided By X 2 11 12 Chegg Com



Find The Value Of K If X K Is The Factor Of The Polynomial X4 Kx2 3x 6k Brainly In


Q Tbn And9gcs1ldbzcasbg22eonj8kqhxytb7kbmljwpdb5wggjq7c478db3p Usqp Cau


Q Tbn And9gctqnv2zy8 Ul0pknyokqomtf6vwlwgvsxubvpkmitgmb8rwvora Usqp Cau


Find The Value Of K If X 1 Is A Factor Of P X In Each Of The Following Cases P X Kx 2 2x 1 Sarthaks Econnect Largest Online Education Community



Find K If X 1 Is A Factor Of P X Kx 2x 2 Brainly In



The Polynomials P X Kx3 3x 3 Q X 3 5x K When Divided By X 4 Leave The Same And 2x Remainde Youtube



If X K Is A Factor Of The Polynomial X 3 Kx 2 3x 15 Find K Math Polynomials Meritnation Com
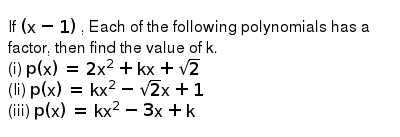


P X Kx 2x 1 Find The Value Of K If X Is 1



The Polynomials P X Kx 3 3x 2 3and Q X 2x 3 5x K When Divided By X 4 Leave The Same Youtube


What Is The Value Of K For Which 3 Is A Root Of The Equation Kx2 7x 3 0 Quora



Value S Of K For Which The Quadratic Equation 2x 2 Kx K 0 Has Equal Roots Is Are Youtube



Ex 2 4 3 Find Value Of K If X 1 Is A Factor Of P X


Given That P D F Of A Random Variable X As Follows F X Kx 1 X For 0 X 1 F X 0 Otherwise Find K And C D F Sarthaks Econnect Largest Online Education Community



Find The Value Of K If Kx 3 9x 2 4x 10 Is Divided By X 3 Leave A Remainder 22


What Is The Value Of K For Which 3 Is A Root Of The Equation Kx2 7x 3 0 Quora



Find The Value Of K If X K Is A Factor Of The Polynomial X3 Kx2 2x K 4 Brainly In



For What Value Of K Is The Polynomial P X 2x Cube Kx Square 3x 10 Exactly Divisible By X 2 Brainly In



Class 9 Polynomial 2 Coordinate Geometry Linear Equation In Two Variables Euclid S Geometry Lines And Angles Notes



Find The Value Of K If X 1 Is A Factor Of P X Kx2 3x 5 Brainly In



If The Polynomial 3x Kx 2x 3 Leaves A Remainder 5 When Divided By X 2 Find The Value Of K Using Brainly In



Rd Sharma Solutions For Class 10 Chapter 8 Quadratic Equations Exercise 8 6 Avail Pdf
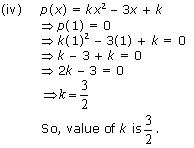


Chapter 2 Polynomials Ncert Solutions For Class 10 Mathematics Maharashtra Topperlearning


For What Value Of K X 1 Is A Factor Of P X Kx 2 X 4 Quora



If One Zeros Of The Quadratic Polynomial Kx 2 3x K Is 2 Then Find The Value Of K



The Probability Distribution Of A Random Variable X Is Given As



Ex 2 4 3 Find Value Of K If X 1 Is A Factor Of P X



Ncert Solutions For Class 9 Maths Chapter 2 Exercise 2 4 Polynomials



Remainder Theorem Examples Video Khan Academy


コメント
コメントを投稿